Županijsko natjecanje iz matematike 2015, SŠ4 A 1
Dodao/la:
arhiva22. ožujka 2015. Neka je
![a = \sqrt[2015]{2015}](/media/m/5/c/1/5c1d3f2e46e6f2edad40993ff57651d3.png)
i neka je
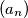
niz takav da je
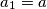
i
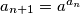
za
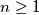
.
Postoji li prirodni broj

takav da je
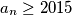
?
%V0
Neka je $a = \sqrt[2015]{2015}$ i neka je $(a_n)$ niz takav da je $a_1 = a$ i $a_{n + 1} = a^{a_n}$ za $n \geq 1$.
Postoji li prirodni broj $n$ takav da je $a_n \geq 2015$?
Izvor: Županijsko natjecanje iz matematike 2015