Državno natjecanje 2005 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. dokazite da postoji tocno jedan prirodan broj koji se u dekadskom sustavu zapisuje samo znamenkama
i
, ima
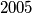
znamenaka i djeljiv je s
.
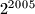
%V0
dokazite da postoji tocno jedan prirodan broj koji se u dekadskom sustavu zapisuje samo znamenkama $2$ i $5$, ima $2005$ znamenaka i djeljiv je s $2^{2005}$.
Izvor: Državno natjecanje iz matematike 2005
Školjka 
