Državno natjecanje 2007 SŠ4 2
Dodao/la:
arhiva1. travnja 2012. Niz
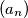
zadan je rekurzivno:
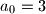

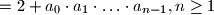
.
a) Dokažite da su svi članovi tog niza u parovima relativno prosti prirodni brojevi.
b) Odredite
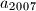
.
%V0
Niz $(a_n)$ zadan je rekurzivno:
$a_0 = 3$
$a_n$ $= 2 + a_0 \cdot a_1 \cdot \ldots \cdot a_{n-1}, n\geq 1$.
a) Dokažite da su svi članovi tog niza u parovima relativno prosti prirodni brojevi.
b) Odredite $a_{2007}$.
Izvor: Državno natjecanje iz matematike 2007