Šiljastokutni trokut kome su , i polovišta stranica , i upisan je u kružnicu sa središtem u točki polumjera . Dokažite da je
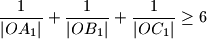
%V0
Šiljastokutni trokut $ABC$ kome su $A_1$, $B_1$ i $C_1$ polovišta stranica $\overline{BC}$, $\overline{CA}$ i $\overline{AB}$ upisan je u kružnicu sa središtem u točki $O$ polumjera $1$. Dokažite da je
$$\frac{1}{|OA_1|}+\frac{1}{|OB_1|}+\frac{1}{|OC_1|} \geq 6$$
Školjka 
kome su 
, 
i 
polovišta stranica 
, 
i 
upisan je u kružnicu sa središtem u točki 
polumjera 
. Dokažite da je