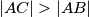
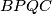
Neka je šiljastokutni trokut u kojem je . Neka je nožište visine iz na stranicu . Neka je točka na produžetku dužine preko vrha te neka je točka na produžetku dužine preko vrha tako da je tetivni četverokut.
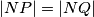
Ako vrijedi , dokaži da je središte kružnice opisane trokutu .
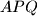
%V0
Neka je $ABC$ šiljastokutni trokut u kojem je $|AC| > |AB|$. Neka je $N$ nožište visine iz $A$ na stranicu $\overline{BC}$. Neka je točka $P$ na produžetku dužine $\overline{AB}$ preko vrha $B$ te neka je točka $Q$ na produžetku dužine $\overline{AC}$ preko vrha $C$ tako da je $BPQC$ tetivni četverokut.
Ako vrijedi $|NP| = |NQ|$, dokaži da je $N$ središte kružnice opisane trokutu $APQ$.
Školjka 
šiljastokutni trokut u kojem je 
. Neka je 
nožište visine iz 
na stranicu 
. Neka je točka 
na produžetku dužine 
preko vrha 
te neka je točka 
na produžetku dužine 
preko vrha 
tako da je 
tetivni četverokut.
, dokaži da je 
.