Slični zadaci
a) Neka je  prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu
prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu  -tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
-tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
b) Postoji li aritmetički niz čija je razlika prirodni broj koji sadrži beskonačno mnogo kubova prirodnih brojeva, ali ne sadrži niti jedan kvadrat prirodnog broja?
 prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu
prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu  -tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
-tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.b) Postoji li aritmetički niz čija je razlika prirodni broj koji sadrži beskonačno mnogo kubova prirodnih brojeva, ali ne sadrži niti jedan kvadrat prirodnog broja?
Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 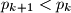 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 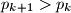 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 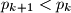 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 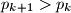 .
.  Školjka
Školjka  neka je
neka je 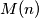 najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva
najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva 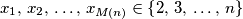 tako da vrijedi:
tako da vrijedi: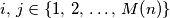 brojevi
brojevi 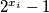 i
i 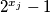 su relativno prosti.
su relativno prosti.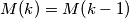 za neki prirodni broj
za neki prirodni broj  , dokaži da je
, dokaži da je 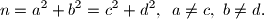
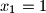 ,
, 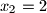 ,
, 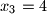 ,
, 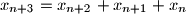 , za svako
, za svako  . Dokažite da se svaki prirodni broj može prikazati kao zbroj različitih elemenata tog niza.
. Dokažite da se svaki prirodni broj može prikazati kao zbroj različitih elemenata tog niza. 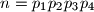 , gdje su
, gdje su 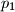 ,
, 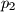 ,
, 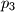 i
i 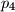 četiri različita prosta broja. Njegovi pozitivni cjelobrojni djelitelji su
četiri različita prosta broja. Njegovi pozitivni cjelobrojni djelitelji su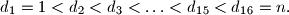
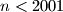 , takav da je
, takav da je 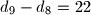 ?
? 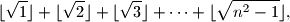 gdje je
gdje je 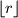 najveći cijeli broj koji nije veći od
najveći cijeli broj koji nije veći od  .
.