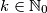
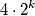
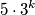
Dokaži da je za svaki moguće odabrati različitih prirodnih brojeva koji nisu veći od , tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.
%V0
Dokaži da je za svaki $k \in \mathbb{N}_0$ moguće odabrati $\displaystyle 4 \cdot 2^k$ različitih prirodnih brojeva koji nisu veći od $\displaystyle 5 \cdot 3^k$, tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.
Školjka 
moguće odabrati 
različitih prirodnih brojeva koji nisu veći od 
, tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.