Školsko/gradsko natjecanje iz matematike 2016, SŠ2 A 7
Kvaliteta:
Avg: 0,0Težina:
Avg: 2,0Neka je 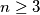 prirodni broj. Kvadrat
prirodni broj. Kvadrat  je podijeljen na
je podijeljen na 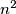 pravokutnika pravcima
pravokutnika pravcima 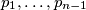 paralelnim s pravcem
paralelnim s pravcem  i pravcima
i pravcima 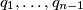 paralelnim s pravcem
paralelnim s pravcem  . Stranice
. Stranice  i
i  leže redom na pravcima
leže redom na pravcima 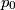 i
i 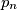 , a stranice
, a stranice  i
i 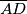 redom na pravcima
redom na pravcima 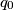 i
i 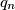 . Pravac
. Pravac  se nalazi između pravaca
se nalazi između pravaca 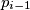 i
i 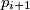 , a pravac
, a pravac 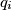 se nalazi između pravaca
se nalazi između pravaca 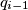 i
i 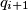 , za sve
, za sve 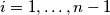 . Neka je
. Neka je 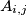 pravokutnik omeđen pravcima
pravokutnik omeđen pravcima 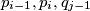 i
i 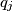 , za
, za 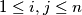 .
.
Ako je poznato da pravokutnici 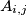 i
i 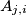 imaju jednake površine za svaki par
imaju jednake površine za svaki par 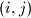 takav da je
takav da je 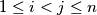 , dokaži da je
, dokaži da je 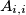 kvadrat za svaki
kvadrat za svaki 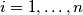 .
.
Izvor: Školsko/gradsko natjecanje iz matematike 2016
 Školjka
Školjka 
