Školsko/gradsko natjecanje iz matematike 2016, SŠ3 A 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 3,0Izvor: Školsko/gradsko natjecanje iz matematike 2016
Komentari:
PrtenjacaSanel, 28. listopada 2019. 12:50
Uvjet iz zadatka bi se mogao protumačiti tako da je 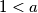 (tj.
(tj. 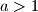 ) i
) i 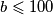 , dakle prema tome bi teoretski
, dakle prema tome bi teoretski  mogao biti bilo koji prirodan broj veći od
mogao biti bilo koji prirodan broj veći od  pa bi zadatak imao beskonačno mnogo rješenja i ne bi bio previše smislen. Ali da, prema službenom rješenju umetnut je zarez između
pa bi zadatak imao beskonačno mnogo rješenja i ne bi bio previše smislen. Ali da, prema službenom rješenju umetnut je zarez između  i
i  kao da nabrajaju brojeve između
kao da nabrajaju brojeve između  i
i  , a ne kao da odvajaju dva intervala. Netko tko ne bi znao riješiti taj zadatak na natjecanju vjerojatno bi pri žalbi mogao izvući svih
, a ne kao da odvajaju dva intervala. Netko tko ne bi znao riješiti taj zadatak na natjecanju vjerojatno bi pri žalbi mogao izvući svih  bodova svojim argumentom :).
bodova svojim argumentom :).
Zar nije 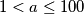 i
i 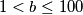 ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:
ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:
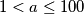 i
i 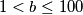 ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:
ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:Zadnja promjena: PrtenjacaSanel, 28. listopada 2019. 14:16
ikicic, 28. listopada 2019. 09:58
Zar nije 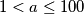 i
i 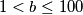 ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:
ocekivano? Tako se barem slaze sa sluzbenim rjesenjem:
PrtenjacaSanel, 21. listopada 2019. 17:13
Zadnja promjena: PrtenjacaSanel, 21. listopada 2019. 17:14
 Školjka
Školjka 

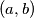 takve da je
takve da je 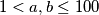 i
i 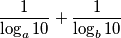 prirodni broj.
prirodni broj. 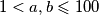 bi trebalo značiti da su
bi trebalo značiti da su