Državno natjecanje iz matematike 2016, SŠ4 A 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0U utrci sudjeluje 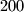 biciklista. Na početku utrke biciklisti su poredani jedan iza drugoga. Kažemo da neki biciklist pretječe ako mijenja mjesto s biciklistom neposredno ispred sebe. Tijekom utrke poredak se mijenja samo kad neki biciklist pretječe.
biciklista. Na početku utrke biciklisti su poredani jedan iza drugoga. Kažemo da neki biciklist pretječe ako mijenja mjesto s biciklistom neposredno ispred sebe. Tijekom utrke poredak se mijenja samo kad neki biciklist pretječe.
Neka je  broj svih mogućih poredaka na kraju utrke u kojoj je svaki biciklist pretjecao točno jednom, te neka je
broj svih mogućih poredaka na kraju utrke u kojoj je svaki biciklist pretjecao točno jednom, te neka je  broj svih mogućih poredaka na kraju utrke u kojoj je svaki biciklist pretjecao najviše jednom. Dokaži da vrijedi
broj svih mogućih poredaka na kraju utrke u kojoj je svaki biciklist pretjecao najviše jednom. Dokaži da vrijedi 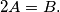
Izvor: Državno natjecanje iz matematike 2016
 Školjka
Školjka 
