Državno natjecanje 2001 SŠ1 4
Dodao/la:
arhiva1. travnja 2012. Za koje se prirodne brojeve

pravokutna ploča
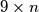
može prekriti pločicama oblika

tako da se one međusobno ne preklapaju?
%V0
Za koje se prirodne brojeve $n$ pravokutna ploča $9 \times n$ može prekriti pločicama oblika $\setlength{\unitlength}{5pt}
\begin{picture}(2, 3)
\put(0, 0){\line(1, 0){1}}
\put(0, 0){\line(0, 1){2}}
\put(2, 2){\line(-1, 0){2}}
\put(2, 2){\line(0, -1){1}}
\put(1, 0){\line(0, 1){2}}
\put(0, 1){\line(1, 0){2}}
\end{picture}$ tako da se one međusobno ne preklapaju?
Izvor: Državno natjecanje iz matematike 2001