Državno natjecanje iz matematike 2017, SŠ4 A 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Dan je šiljastokutni trokut  u kojem vrijedi
u kojem vrijedi 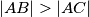 . Neka je
. Neka je  središte kružnice opisane tom trokutu, a
središte kružnice opisane tom trokutu, a 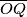 promjer kružnice opisane trokutu
promjer kružnice opisane trokutu 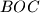 . Pravac paralelan s pravcem
. Pravac paralelan s pravcem  kroz
kroz  siječe pravac
siječe pravac 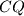 u točki
u točki  , a pravac paralelan s pravcem
, a pravac paralelan s pravcem 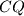 kroz
kroz  siječe pravac
siječe pravac  u točki
u točki  . Neka je
. Neka je  presjek pravaca
presjek pravaca 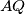 i
i  . Dokaži da točka
. Dokaži da točka  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu 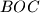 .
.
Izvor: Državno natjecanje iz matematike 2017
 Školjka
Školjka 
