Državno natjecanje 2002 SŠ1 2
Dodao/la:
arhiva1. travnja 2012. Dokažite da za bilo koje pozitivne brojeve

,

,

i bilo koji nenegativan pozitivan broj

vrijedi nejednakost
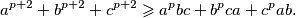
%V0
Dokažite da za bilo koje pozitivne brojeve $a$, $b$, $c$ i bilo koji nenegativan pozitivan broj $p$ vrijedi nejednakost $$a^{p+2} + b^{p+2} + c^{p+2} \geqslant a^pbc + b^pca + c^pab \text{.}$$
Izvor: Državno natjecanje iz matematike 2002