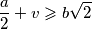
U jednakokračnom trokutu duljina osnovice je , duljina kraka , duljina visine na osnovicu , pri čemu vrijedi: . Odredite kutove trokuta. Kolika je površina trokuta ako je ?
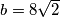
%V0
U jednakokračnom trokutu duljina osnovice je $a$, duljina kraka $b$, duljina visine na osnovicu $v$, pri čemu vrijedi: $\displaystyle \frac{a}{2} + v \geqslant b\sqrt2$. Odredite kutove trokuta. Kolika je površina trokuta ako je $ b = 8\sqrt2 $?
Školjka 
, duljina kraka 
, duljina visine na osnovicu 
, pri čemu vrijedi: 
. Odredite kutove trokuta. Kolika je površina trokuta ako je 
?