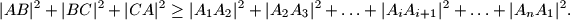Slični zadaci
Oko kružnice polumjera  položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.
 položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.  Školjka
Školjka  na kružnicu diraju je u točkama
na kružnicu diraju je u točkama  i
i  . Neka je
. Neka je  na kružnici, različita od
na kružnici, različita od 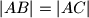 . Dokažite da je
. Dokažite da je 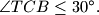
 i
i  na koje su povučene dvije unutarnje zajedničke tangente
na koje su povučene dvije unutarnje zajedničke tangente  ,
, 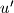 i dvije vanjske
i dvije vanjske  ,
, 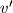 . Dokažite da sjecišta tangenata
. Dokažite da sjecišta tangenata 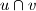 ,
, 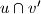 ,
, 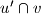 ,
, 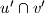 leže na jednoj kružnici.
leže na jednoj kružnici. 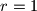 postavljeno je unutar kružnice polumjera
postavljeno je unutar kružnice polumjera  i
i  redom opseg i površina pravokutnika. Dokaži da vrijedi
redom opseg i površina pravokutnika. Dokaži da vrijedi 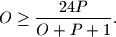
 paralelna je s promjerom
paralelna je s promjerom 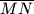 kružnice. Neka je
kružnice. Neka je  tangenta te kružnice u točki
tangenta te kružnice u točki  te neka su točke
te neka su točke  redom sjecišta pravaca
redom sjecišta pravaca 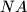 i
i 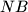 s pravcem
s pravcem 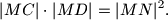
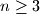 prirodni broj. U kružnicu je upisan
prirodni broj. U kružnicu je upisan  -terokut
-terokut 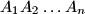 . Dokaži da postoje tri vrha
. Dokaži da postoje tri vrha 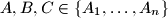 za koje vrijedi
za koje vrijedi