MEMO 2019 pojedinačno zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  šiljastokutni trokut s opisanom kružnicom
šiljastokutni trokut s opisanom kružnicom  u kojem je
u kojem je 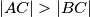 . Pretpostavimo da je
. Pretpostavimo da je  točka na
točka na  takva da je
takva da je 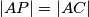 i da je
i da je  unutarnja točka kraćeg luka
unutarnja točka kraćeg luka 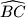 kružnice
kružnice  . Neka je
. Neka je  sjecište pravaca
sjecište pravaca 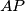 i
i  . Nadalje, pretpostavimo da je
. Nadalje, pretpostavimo da je  točka na
točka na  takva da je
takva da je 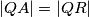 i da je
i da je  unutarnja točka kraćeg luka
unutarnja točka kraćeg luka 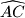 kružnice
kružnice  . Konačno, neka je
. Konačno, neka je  sjecište pravca
sjecište pravca  i simetrale stranice
i simetrale stranice  . Dokaži da su točke
. Dokaži da su točke  ,
,  ,
,  i
i  konciklične.
konciklične.
Izvor: Srednjoeuropska matematička olimpijada 2019, pojedinačno natjecanje, problem 3
 Školjka
Školjka 
