Državno natjecanje iz matematike 1993, SŠ4 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0U trokutu s duljinama stranica  i nasuprotnim kutovima
i nasuprotnim kutovima 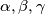 definira se tzv. Brocardov kut
definira se tzv. Brocardov kut  formulom
formulom 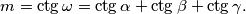 (a) Izrazite zbrojeve
(a) Izrazite zbrojeve 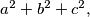
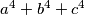 i
i 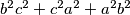 pomoću veličine
pomoću veličine  i površine
i površine  trokuta koristeći prethodno dokazanu formulu
trokuta koristeći prethodno dokazanu formulu 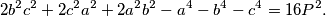 (b) Dokažite da je
(b) Dokažite da je 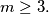 Što to znači za kut
Što to znači za kut 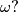 Za koje trokute vrijedi jednakost?
Za koje trokute vrijedi jednakost?
(c) Dokažite da ne postoji trokut kod kojeg su 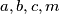 cijeli brojevi.
cijeli brojevi.
Izvor: Državno natjecanje iz matematike 1993
 Školjka
Školjka 
