Državno natjecanje iz matematike 2019, SŠ1 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0U jednakokračnom trokutu 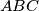 vrijedi
vrijedi 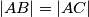 i
i 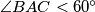 . Neka je točka
. Neka je točka 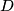 na dužini
na dužini 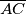 takva da je
takva da je 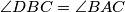 , neka je
, neka je 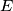 sjecište simetrale dužine
sjecište simetrale dužine 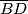 i paralele s
i paralele s 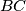 kroz točku
kroz točku 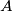 te neka je
te neka je 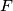 točka na pravcu
točka na pravcu 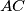 takva da se
takva da se 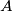 nalazi između
nalazi između 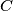 i
i 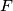 i vrijedi
i vrijedi 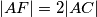 .
.
a) Dokaži da su pravci 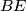 i
i 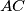 paralelni.
paralelni.
b) Dokaži da se okomica iz 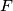 na
na 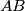 i okomica iz
i okomica iz 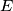 na
na 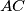 sijeku na pravcu
sijeku na pravcu 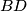 .
.
U a) dijelu zadatka dozvoljeno je korištenje tvrdnje iz b) čak i ako nije dokazana.
Izvor: Državno natjecanje iz matematike 2019
 Školjka
Školjka 
