Državno natjecanje 2005 SŠ1 3
Dodao/la:
arhiva1. travnja 2012. Koju najveću vrijednost može poprimiti izraz
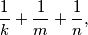
ako su

,

,

prirodni brojevi takvi da je
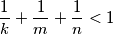
.
%V0
Koju najveću vrijednost može poprimiti izraz $$\frac{1}{k} + \frac{1}{m} + \frac{1}{n} \text{,}$$ ako su $k$, $m$, $n$ prirodni brojevi takvi da je $\displaystyle \frac{1}{k} + \frac{1}{m} + \frac{1}{n} < 1$.
Izvor: Državno natjecanje iz matematike 2005