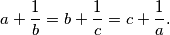
Neka su , , realni brojevi koji nisu svi jednaki, takvi da vrijedi Dokaži da je .
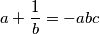
%V0
Neka su $a$, $b$, $c$ realni brojevi koji nisu svi jednaki, takvi da vrijedi $$a+\frac1b=b+\frac1c=c+\frac1a \text{.}$$ Dokaži da je $\displaystyle a+\frac1b=-abc$.
Školjka 
, 
, 
realni brojevi koji nisu svi jednaki, takvi da vrijedi 
Dokaži da je 
.