Neka je polumjer kugle opisane oko pravilne četverostrane piramide, a polumjer kugle upisane u tu piramidu. Dokaži da je
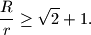
%V0
Neka je $R$ polumjer kugle opisane oko pravilne četverostrane piramide, a $r$ polumjer kugle upisane u tu piramidu. Dokaži da je $$
\dfrac{R}{r}\geq\sqrt{2}+1.
$$
Školjka 
polumjer kugle opisane oko pravilne četverostrane piramide, a 
polumjer kugle upisane u tu piramidu. Dokaži da je 