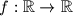
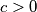
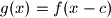
Ako je parna fukcija i ako je za funkcija neparna, dokažite da je periodička funkcija s periodom .
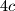
%V0
Ako je $f : \mathbb{R} \to \mathbb{R}$ parna fukcija i ako je za $c > 0$ funkcija $g(x) = f(x - c)$ neparna, dokažite da je $f$ periodička funkcija s periodom $4c$.
Školjka 
parna fukcija i ako je za 
funkcija 
neparna, dokažite da je 
periodička funkcija s periodom 
.