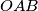
Na polupravcima i sa zajedničkim početkom dane su točke i (na ) te i (na ). Ako je pravac paralelan s težišnicom trokuta , dokažite da je pravac paralelan s težišnicom trokuta .
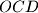
%V0
Na polupravcima $p$ i $q$ sa zajedničkim početkom $O$ dane su točke $A$ i $C$ (na $p$) te $B$ i $D$ (na $q$). Ako je pravac $CD$ paralelan s težišnicom trokuta $OAB$, dokažite da je pravac $AB$ paralelan s težišnicom trokuta $OCD$.
Školjka 
i 
sa zajedničkim početkom 
dane su točke 
i 
(na 
i 
(na 
paralelan s težišnicom trokuta 
, dokažite da je pravac 
paralelan s težišnicom trokuta 
.