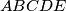
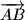
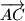
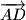
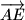
Neka je konveksan peterokut. Translacijama za vektore , , , dobivamo četiri nova peterokuta. Dokažite da među tih pet peterokuta postoje dva koja imaju barem jednu zajedničku unutarnju točku.
%V0
Neka je $ABCDE$ konveksan peterokut. Translacijama za vektore $\overrightarrow{AB}$, $\overrightarrow{AC}$, $\overrightarrow{AD}$, $\overrightarrow{AE}$ dobivamo četiri nova peterokuta. Dokažite da među tih pet peterokuta postoje dva koja imaju barem jednu zajedničku unutarnju točku.
Školjka 
konveksan peterokut. Translacijama za vektore 
, 
, 
, 
dobivamo četiri nova peterokuta. Dokažite da među tih pet peterokuta postoje dva koja imaju barem jednu zajedničku unutarnju točku.