Županijsko natjecanje 1996 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. U trokutu
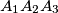
označimo:
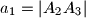
,
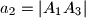
,
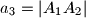
. Duljine visina tog trokuta iz vrhova

,
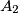
,
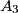
označimo redom sa
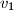
,
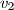
,
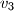
. Promatrajmo sve brojeve oblika
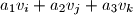
gdje je
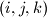
bilo koja permutacija skupa
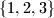
. Nađite najmanji od tih brojeva i izrazite ga pomoću površine

trokuta
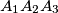
.
%V0
U trokutu $A_1A_2A_3$ označimo: $a_1=|A_2A_3|$, $a_2=|A_1A_3|$, $a_3=|A_1A_2|$. Duljine visina tog trokuta iz vrhova $A_1$, $A_2$, $A_3$ označimo redom sa $v_1$, $v_2$, $v_3$. Promatrajmo sve brojeve oblika $a_1v_i + a_2v_j + a_3v_k$ gdje je $(i, j, k)$ bilo koja permutacija skupa $\{1, 2, 3\}$. Nađite najmanji od tih brojeva i izrazite ga pomoću površine $P$ trokuta $A_1A_2A_3$.
Izvor: Županijsko natjecanje iz matematike 1996