HMO 2023 - Izborni test za IMO - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  tetivni četverokut. Neka su
tetivni četverokut. Neka su  i
i  redom polovišta dužina
redom polovišta dužina  i
i 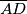 . Pretpostavimo da točke
. Pretpostavimo da točke 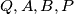 leže na pravcu u tom poretku, da je
leže na pravcu u tom poretku, da je  tangenta opisane kružnice trokuta
tangenta opisane kružnice trokuta 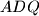 te da je
te da je  tangenta opisane kružnice trokuta
tangenta opisane kružnice trokuta 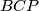 . Dokaži da se pravac
. Dokaži da se pravac  , tangenta opisane kružnice trokuta
, tangenta opisane kružnice trokuta 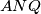 u točki
u točki  i tangenta opisane kružnice trokuta
i tangenta opisane kružnice trokuta 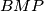 u točki
u točki  sijeku u jednoj točki.
sijeku u jednoj točki.
Izvor: Hrvatska matematička olimpijada 2023.
 Školjka
Školjka 
