Državno natjecanje 2007 SŠ1 3
Dodao/la:
arhiva1. travnja 2012. a) Dokažite da se ploča dimenzija
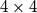
može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.
b) Dokažite da gore navedeno svojstvo ne vrijedi za ploču dimenzija
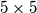
.
%V0
a) Dokažite da se ploča dimenzija $4 \times 4$ može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.
b) Dokažite da gore navedeno svojstvo ne vrijedi za ploču dimenzija $5 \times 5$.
Izvor: Državno natjecanje iz matematike 2007