Županijsko natjecanje 1998 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. Dokažite da ne postoji funkcija
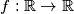
koja zadovoljava ove uvjete:
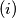
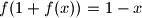
, za svaki
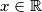
,
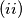
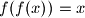
, za svaki
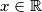
.
%V0
Dokažite da ne postoji funkcija $f : \mathbb{R} \rightarrow \mathbb{R}$ koja zadovoljava ove uvjete:
$(i)$ $f(1 + f(x)) = 1 - x$, za svaki $x \in \mathbb{R}$,
$(ii)$ $f(f(x)) = x$, za svaki $x \in \mathbb{R}$.
Izvor: Županijsko natjecanje iz matematike 1998