HMO 2013 - Prvi dan - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Dan je šiljastokutan trokut  s ortocentrom
s ortocentrom  . Neka je
. Neka je  točka takva da je četverokut
točka takva da je četverokut 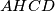 paralelogram. Neka je
paralelogram. Neka je  okomica na pravac
okomica na pravac  kroz polovište
kroz polovište  stranice
stranice  . Označimo sjecište pravaca
. Označimo sjecište pravaca  i
i  s
s  , a polovište dužine
, a polovište dužine 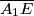 s
s  . Točku u kojoj paralela s pravcem
. Točku u kojoj paralela s pravcem  kroz točku
kroz točku  siječe
siječe  označimo s
označimo s  . Dokaži da je četverokut
. Dokaži da je četverokut 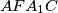 tetivan ako i samo ako pravac
tetivan ako i samo ako pravac 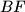 prolazi polovištem dužine
prolazi polovištem dužine 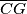 .
.
Izvor: Hrvatska matematička olimpijada 2013.
 Školjka
Školjka 
