HMO 2013 - Izborni test za MEMO - Zadatak 1
Dodao/la:
arhiva17. listopada 2023. Neka su 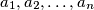 pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 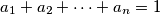 .
.
Dokaži nejednakost: 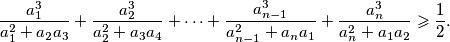
Neka su $a_1,a_2,\ldots,a_n$ pozitivni realni brojevi takvi da je $a_1+a_2+\cdots+a_n=1$.
Dokaži nejednakost:
$$\frac{a_1^3}{a_1^2+a_2a_3}+\frac{a_2^3}{a_2^2+a_3a_4}+\dotsb
+\frac{a_{n-1}^3}{a_{n-1}^2+a_na_1}
+\frac{a_n^3}{a_n^2+a_1a_2}\geqslant \frac{1}{2}.$$
Izvor: Hrvatska matematička olimpijada 2013.