HMO 2013 - Izborni test za IMO - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Dan je jednakokračni trokut  s osnovicom
s osnovicom  . Točka
. Točka  na stranici
na stranici  i točka
i točka  na stranici
na stranici  odabrane su tako da je
odabrane su tako da je 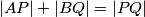 . Paralela s pravcem
. Paralela s pravcem  kroz polovište dužine
kroz polovište dužine 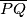 siječe dužinu
siječe dužinu  u točki
u točki  . Kružnica opisana trokutu
. Kružnica opisana trokutu 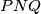 siječe pravac
siječe pravac  u točkama
u točkama  i
i  , a pravac
, a pravac  u točkama
u točkama  i
i  . Ako je točka
. Ako je točka  sjecište pravaca
sjecište pravaca 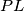 i
i 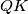 , dokaži da je pravac
, dokaži da je pravac  okomit na pravac
okomit na pravac 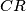 .
.
Izvor: Hrvatska matematička olimpijada 2013.
 Školjka
Školjka 
