Županijsko natjecanje 1999 SŠ4 2
Dodao/la:
arhiva1. travnja 2012. Dokažite da za svaki prirodni broj

vrijedi jednakost
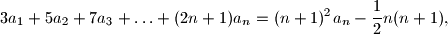
ako je
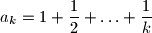
, za svaki prirodni broj

.
%V0
Dokažite da za svaki prirodni broj $n$ vrijedi jednakost $$
3a_1+5a_2+7a_3+\ldots+(2n+1)a_n
=(n+1)^2a_n -\dfrac{1}{2}n(n+1),
$$ ako je $ {a_k=1+\dfrac{1}{2}+\ldots+\dfrac{1}{k}}$, za svaki prirodni broj $k$.
Izvor: Županijsko natjecanje iz matematike 1999