HMO 2015 - Drugi dan - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0U šiljastokutnom trokutu  vrijedi
vrijedi 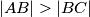 , a točke
, a točke  i
i  su redom nožišta visina iz vrhova
su redom nožišta visina iz vrhova  i
i  . Neka je
. Neka je  drugo sjecište kružnica opisanih trokutima
drugo sjecište kružnica opisanih trokutima  i
i 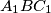 (različito od
(različito od  ). Neka je
). Neka je  sjecište tangenata na opisanu kružnicu trokuta
sjecište tangenata na opisanu kružnicu trokuta  u točkama
u točkama  i
i  , te neka se pravci
, te neka se pravci 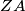 i
i 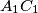 sijeku u točki
sijeku u točki  , a pravci
, a pravci 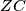 i
i 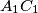 u točki
u točki  .
.
Dokaži da točka  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu 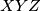 .
.
Izvor: Hrvatska matematička olimpijada 2015.
 Školjka
Školjka 
