HMO 2016 - Izborni test za MEMO - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Dan je tetivni četverokut  . Polupravci
. Polupravci  i
i  sijeku se u točki
sijeku se u točki  . U unutrašnjosti trokuta
. U unutrašnjosti trokuta 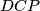 dana je točka
dana je točka  takva da pravac
takva da pravac 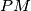 raspolavlja kut
raspolavlja kut 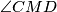 . Pravac
. Pravac 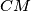 siječe kružnicu opisanu trokutu
siječe kružnicu opisanu trokutu 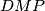 ponovno u točki
ponovno u točki  , a pravac
, a pravac 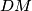 siječe kružnicu opisanu trokutu
siječe kružnicu opisanu trokutu 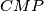 ponovno u točki
ponovno u točki  .
.
1) Dokaži da dužine 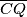 i
i 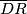 imaju jednaku duljinu.
imaju jednaku duljinu.
2) Dokaži da trokuti 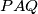 i
i 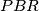 imaju jednaku površinu.
imaju jednaku površinu.
Izvor: Hrvatska matematička olimpijada 2016.
 Školjka
Školjka 
