HMO 2017 - Izborni test za MEMO - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Neka je 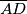 visina šiljastokutnog trokuta
visina šiljastokutnog trokuta  . Na pravcu
. Na pravcu  nalaze se međusobno različite točke
nalaze se međusobno različite točke  i
i  takve da vrijedi
takve da vrijedi 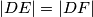 i pritom je točka
i pritom je točka  u unutrašnjosti trokuta
u unutrašnjosti trokuta  . Kružnica opisana trokutu
. Kružnica opisana trokutu 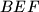 siječe dužine
siječe dužine  i
i  redom u točkama
redom u točkama  i
i  . Kružnica opisana trokutu
. Kružnica opisana trokutu 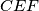 siječe dužine
siječe dužine  i
i  redom u točkama
redom u točkama  i
i  .
.
Dokaži da se pravci  ,
, 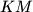 i
i 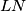 sijeku u jednoj točki.
sijeku u jednoj točki.
Izvor: Hrvatska matematička olimpijada 2017.
 Školjka
Školjka 
