HMO 2018 - Drugi dan - Zadatak 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Neka je 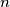 prirodni broj. Unutar kružnice nalaze se točke
prirodni broj. Unutar kružnice nalaze se točke 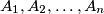 , a na kružnici točke
, a na kružnici točke 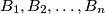 takve da su dužine
takve da su dužine  u parovima disjunktne. Skakavac smije skočiti iz točke
u parovima disjunktne. Skakavac smije skočiti iz točke  u točku
u točku 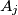 (za
(za 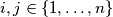 ,
, 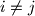 ) ako i samo ako dužina
) ako i samo ako dužina  ne prolazi nijednom unutarnjom točkom dužina
ne prolazi nijednom unutarnjom točkom dužina  .
.
Pokaži da skakavac nizom skokova može doći iz bilo koje točke  u bilo koju točku
u bilo koju točku 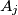 .
.
Izvor: Hrvatska matematička olimpijada 2018.
 Školjka
Školjka 
