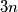
Dokažite da se vrhovi -terostrane prizme mogu obojati s tri boje na takav način da svaki vrh bude spojen bridovima s vrhovima svih triju boja. Dokažite da ako se vrhovi -terostrane prizme mogu obojati s tri boje tako da je svaki vrh spojen bridovima s vrhovima svih triju boja, onda je djeljiv s .
%V0
$a)$ Dokažite da se vrhovi $3n$-terostrane prizme mogu obojati s tri boje na takav način da svaki vrh bude spojen bridovima s vrhovima svih triju boja.
$b)$ Dokažite da ako se vrhovi $n$-terostrane prizme mogu obojati s tri boje tako da je svaki vrh spojen bridovima s vrhovima svih triju boja, onda je $n$ djeljiv s $3$.
Školjka 
Dokažite da se vrhovi 
-terostrane prizme mogu obojati s tri boje na takav način da svaki vrh bude spojen bridovima s vrhovima svih triju boja.
Dokažite da ako se vrhovi 
-terostrane prizme mogu obojati s tri boje tako da je svaki vrh spojen bridovima s vrhovima svih triju boja, onda je 
.