HMO 2021 - Prvi dan - Zadatak 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Za svaki prost broj  negdje u svemiru postoji planet
negdje u svemiru postoji planet 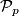 u čijem se oceanu nalazi točno
u čijem se oceanu nalazi točno  otoka,
otoka, 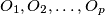 . Između otoka
. Između otoka 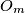 i
i 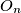 (za
(za 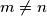 ) postoji most ako i samo ako je broj
) postoji most ako i samo ako je broj 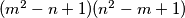 djeljiv s
djeljiv s  . S mosta nije moguće prijeći direktno na drugi most već samo na otok.
. S mosta nije moguće prijeći direktno na drugi most već samo na otok.
Dokaži da postoji beskonačno mnogo prostih brojeva  za koje na planetu
za koje na planetu 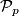 nije moguće sa svakog otoka doći na svaki drugi krećući se samo po otocima i mostovima.
nije moguće sa svakog otoka doći na svaki drugi krećući se samo po otocima i mostovima.
Izvor: Hrvatska matematička olimpijada 2021.
 Školjka
Školjka 
