HMO 2021 - Izborni test za IMO - Zadatak 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Neka je  prirodan broj i neka je
prirodan broj i neka je 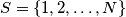 . Neka su
. Neka su  međusobno različiti realni brojevi takvi da za sve
međusobno različiti realni brojevi takvi da za sve 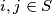 vrijedi: ako je
vrijedi: ako je 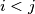 , onda je
, onda je 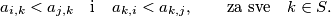
Neka je  prirodan broj takav da je
prirodan broj takav da je 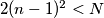 . Dokaži da postoje
. Dokaži da postoje  -člani podskupovi
-člani podskupovi  takvi da vrijedi jedna od sljedeće dvije tvrdnje:
takvi da vrijedi jedna od sljedeće dvije tvrdnje:
(a) za sve 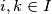 vrijedi: ako je
vrijedi: ako je 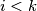 , onda je
, onda je  , za sve
, za sve 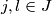 ,
,
(b) za sve 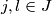 vrijedi: ako je
vrijedi: ako je 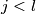 , onda je
, onda je  , za sve
, za sve 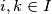 .
.
Izvor: Hrvatska matematička olimpijada 2021.
 Školjka
Školjka 
