Državno natjecanje 2008 SŠ1 1
Dodao/la:
arhiva1. travnja 2012. Neka su

,

,

proizvoljni realni brojevi. Dokaži da je barem jedan od brojeva
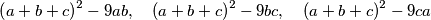
nenegativan.
%V0
Neka su $a$, $b$, $c$ proizvoljni realni brojevi. Dokaži da je barem jedan od brojeva $$\left(a+b+c\right)^2 - 9ab \text{,} \quad \left(a+b+c\right)^2 - 9bc \text{,} \quad \left(a+b+c\right)^2 - 9ca$$ nenegativan.
Izvor: Državno natjecanje iz matematike 2008