Županijsko natjecanje 2004 SŠ4 2
Dodao/la:
arhiva2. travnja 2012. Za svaki prirodan broj

funkcija
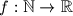
zadovoljava uvjet
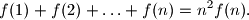
Ako je
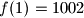
, odredite
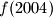
.
%V0
Za svaki prirodan broj $n$ funkcija $f : \mathbb{N} \rightarrow \mathbb{R}$ zadovoljava uvjet $$
f(1)+f(2)+\ldots +f(n)=n^2f(n).
$$ Ako je $f(1)=1002$, odredite $f(2004)$.
Izvor: Županijsko natjecanje iz matematike 2004