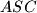
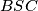
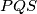
Neka je točka na stranici danog šiljastokutnog trokuta i neka su i središta kružnica opisanih trokutima i . Odredite položaj točke (na stranici ) tako da trokut ima najmanju moguću površinu.
%V0
Neka je $S$ točka na stranici $\overline{AB}$ danog šiljastokutnog trokuta $ABC$ i neka su $P$ i $Q$ središta kružnica opisanih trokutima $ASC$ i $BSC$. Odredite položaj točke $S$ (na stranici $\overline{AB}$) tako da trokut $PQS$ ima najmanju moguću površinu.
Školjka 
točka na stranici 
danog šiljastokutnog trokuta 
i neka su 
i 
središta kružnica opisanih trokutima 
i 
. Odredite položaj točke 
ima najmanju moguću površinu.