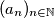
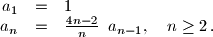
Niz zadan je rekurzivno: Dokažite da su svi članovi tog niza prirodni brojevi.
%V0
Niz $(a_n)_{n \in \mathbb{N}}$ zadan je rekurzivno: $$
\begin{array}{rcl}
a_1&=&1\\
a_n&=&{4n-2\over n} \,\,\, a_{n-1},\quad n\ge 2 \, .
\end{array}
$$ Dokažite da su svi članovi tog niza prirodni brojevi.
Školjka 
zadan je rekurzivno: 
Dokažite da su svi članovi tog niza prirodni brojevi.