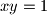
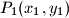
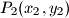
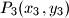
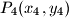
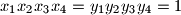
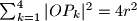
Neka kružnica polumjera siječe hiperbolu u četiri točke ,break , , . Dokaži da vrijedi: , ( je ishodište koordinatnog sustava).
%V0
Neka kružnica polumjera $r$ siječe hiperbolu $xy=1$ u četiri točke $P_1(x_1,y_1)$,\break $P_2(x_2,y_2)$, $P_3(x_3,y_3)$, $P_4(x_4,y_4)$. Dokaži da vrijedi:
$a)$ $x_1x_2x_3x_4=y_1y_2y_3y_4=1$,
$b)$ ${\sum _{k=1}^4|OP_k|^2=4r^2}$ ($O$ je ishodište koordinatnog sustava).
Školjka 
siječe hiperbolu 
u četiri točke 
,break 
, 
, 
. Dokaži da vrijedi:
,
(
je ishodište koordinatnog sustava).