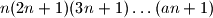
Neka je prirodni broj veći od . Dokaži da je broj djeljiv sa svim prostim brojevima manjim od , za svaki prirodan broj .
%V0
Neka je $a$ prirodni broj veći od $1$. Dokaži da je broj $$
n(2n+1)(3n+1)\dots (an+1)
$$ djeljiv sa svim prostim brojevima manjim od $a$, za svaki prirodan broj $n$.
Školjka 
prirodni broj veći od 
. Dokaži da je broj 
djeljiv sa svim prostim brojevima manjim od 
.