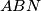
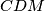
Zadan je konveksan četverokut koji nije paralelogram. Neka pravac koji prolazi kroz polovišta dijagonala četverokuta siječe stranice i redom u točkama i . Dokaži da trokuti i imaju jednake površine.
%V0
Zadan je konveksan četverokut $ABCD$ koji nije paralelogram. Neka pravac koji prolazi kroz polovišta dijagonala četverokuta siječe stranice $\overline{AB}$ i $\overline{CD}$ redom u točkama $M$ i $N$. Dokaži da trokuti $ABN$ i $CDM$ imaju jednake površine.
Školjka 
koji nije paralelogram. Neka pravac koji prolazi kroz polovišta dijagonala četverokuta siječe stranice 
i 
redom u točkama 
i 
. Dokaži da trokuti 
i 
imaju jednake površine.