Državno natjecanje 2009 SŠ1 3
Dodao/la:
arhiva1. travnja 2012. Neka su

,

,

pozitivni realni brojevi, takvi da je
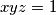
. Dokaži da vrijedi
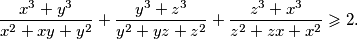
%V0
Neka su $x$, $y$, $z$ pozitivni realni brojevi, takvi da je $xyz = 1$. Dokaži da vrijedi $$ \frac{x^{3} + y^{3}}{x^{2} + xy + y^{2}} + \frac{y^{3} + z^{3}}{y^{2} + yz + z^{2}} + \frac{z^{3} + x^{3}}{z^{2} + zx + x^{2}} \geqslant 2 \text{.} $$
Izvor: Državno natjecanje iz matematike 2009