Općinsko natjecanje 1998 SŠ1 1
Dodao/la:
arhiva2. travnja 2012. U trokutu

je
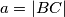
,
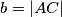
,
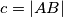
.
Dokažite da je duljina
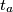
, težišnice iz vrha

, jednaka
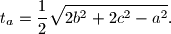
%V0
U trokutu $ABC$ je $a = |BC|$, $b = |AC|$, $c = |AB|$.
Dokažite da je duljina $t_a$, težišnice iz vrha $A$, jednaka $$t_a = \frac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}\text{.}$$
Izvor: Općinsko natjecanje iz matematike 1998