Općinsko natjecanje 1999 SŠ1 1
Dodao/la:
arhiva2. travnja 2012. Ako su

,

i

realni brojevi, takvi da je
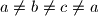
, dokažite da je
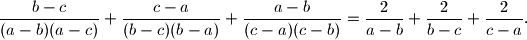
%V0
Ako su $a$, $b$ i $c$ realni brojevi, takvi da je $a\ne b\ne
c\ne a$, dokažite da je $$\frac{b-c}{(a-b)(a-c)} + \frac{c-a}{(b-c)(b-a)} + \frac{a-b}{(c-a)(c-b)} = \frac{2}{a-b} + \frac{2}{b-c} + \frac{2}{c-a}\text{.}$$
Izvor: Općinsko natjecanje iz matematike 1999