Općinsko natjecanje 1999 SŠ1 2
Dodao/la:
arhiva2. travnja 2012. Iz bilo koje točke

unutar jednakostraničnog trokuta

spuštene su okomice
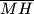
,
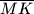
,
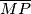
, na njegove stranice

,

,

redom. Dokažite da je
a)
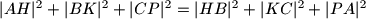
;
b)
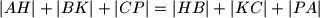
.
%V0
Iz bilo koje točke $M$ unutar jednakostraničnog trokuta $ABC$ spuštene su okomice $\overline{MH}$, $\overline{MK}$, $\overline{MP}$, na njegove stranice $\overline{AB}$, $\overline{BC}$, $\overline{CA}$ redom. Dokažite da je
a) $|AH|^2+|BK|^2+|CP|^2=|HB|^2+|KC|^2+|PA|^2$;
b) $|AH|+|BK|+|CP|=|HB|+|KC|+|PA|$.
Izvor: Općinsko natjecanje iz matematike 1999